LASER(通过教育和研究连接艺术和科学)旨在通过STEAM体验改革火狐体育的数学和物理教育状况,其中包括(i)在我们的物理和数学课程中创新的教学实践,(ii)让学生参与研究,(iii)开发新课程,所有这些都在科学和艺术的界面上。这个想法是利用艺术的普遍吸引力和艺术学科中公认的成功的创造性元素来改革物理和数学的教学方式。


项目
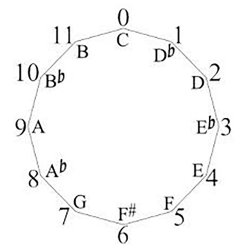

音乐中的对称组
数学家和音乐家都很早就注意到,音乐中的音高等级与整数对12取模(Z_12)有关,例如,将0取为C,形成所谓的音乐时钟。这种识别允许使用抽象代数来模拟音乐事件和研究音乐安排。作曲家M.巴比特是最早使用群论来分析音乐作品的音乐家之一。例如,在巴赫的著名作品《赋格》中,作曲家使用了换位和转位作为创作工具:换位将一系列音高向上或向下移动,而转位则反映了围绕固定轴的旋律。从数学上讲,这些变换表示函数Tn:Z12→Z12,其中Tn(x) = x + n(mod 12); In:Z12→Z12,其中In(x) = -x + n(mod 12)。这两者产生了24阶的二面体群,这是一组规则的12形对称,如上图所示。这群人的行为产生了对古典作品的复杂诠释:贝多芬的第九交响曲可以被看作是圆环上的一条路径。这个项目的目的是用群论来分析古典音乐,发现特定作曲家的技巧和结构,并在学习抽象代数的同时创作新的音乐。
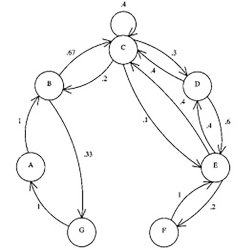
使用随机过程建模爵士乐风格
甚至在计算机发明之前,利用自动算法制作音乐就已经吸引了科学家。在20世纪50年代早期,Iannis Xenakis开始对随机过程进行实验,并利用它们在没有计算机的情况下手工创作音乐作品。第一部完全由电脑生成的作品《伊利亚克弦乐四重奏组曲》由勒雅伦·希勒于1956年出版。从那时起,许多数学和计算方法被用来制作各种风格和形式的音乐。爵士乐是最迷人的音乐风格之一,大量使用即兴创作、多节奏、切分音和摇摆音符。爵士乐独奏背后的即兴音乐的明显随机性可以用马尔可夫链数学建模。马尔可夫链是描述一系列可能事件的随机模型,其中每个事件的概率仅取决于前一个事件所达到的状态。一阶马尔可夫链考虑之前的结果,二阶链考虑两个之前的结果,以此类推。一阶马尔可夫过程的概率表或状态图可以通过找出每个音符在现有乐曲中出现在任何其他音符之后的概率来形成。上面的图给出了这样一个状态图的例子。这种方法用于从现有歌曲中生成新音乐已经有一段时间了。该项目正在进行中,目前正在模仿迈尔斯·戴维斯、约翰·科尔特兰和乔治·本森对迈尔斯·戴维斯创作的歌曲So what的独奏风格。未来的计划包括使用其他类似的确定性和随机算法作曲工具来模拟爵士音乐家,并以类似的风格创作新的音乐作品。
歌唱中的流体:提高歌剧演唱家训练的科学途径
当空气从肺部流出并在喉部产生压降时,人类唱歌或说话的声音就产生了。由于这种压力的变化,声带开始横向振荡,调节空气的压力和流量并发出声音。这种最初的原始声音通过口腔形状和大小的变化,舌头的位置和轮廓以及其他考虑因素进一步控制和修改。从数学的角度来看,这个复杂系统是一个流固耦合问题,用Navier - Stokes方程来描述。
ρ(∂u⁄∂u•∇t + u) -μ(∇u +∇Tu) +∇p = F∇•u = 0ρ∂2我们⁄∂t2 -∇•σ=阵线
这是一个高度非线性的偏微分方程组,很难用解析方法求解,大多数情况下是不可能的。虽然这个问题自20世纪40年代以来一直在研究,但远没有得到解决。我在这个项目中的目标是创建声乐的物理和数值模型,以改善火狐体育音乐学院对歌剧演唱家的培训。
绘画流体动力学
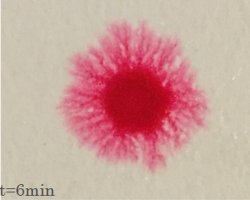
在他1908年的经典研究中,A.M.沃辛顿通过可视化实验详细描述了水花及其形成过程。最近,人们对这个问题重新产生了兴趣,沃辛顿实验背后的许多潜在物理原理现在已经得到澄清。这篇论文的灵感来自最近的一组研究,涉及杰克逊·波洛克(Jackson Pollock)水滴画背后的流体动力学。隐藏在他作品中的物理过程和数学结构受到了严肃的关注,并使艺术的科学追求成为一个引人注目的探索领域。我们目前的工作是探索水彩与水彩纸的相互作用,目的是在这种理解的基础上提供和开发新的艺术作品。具体来说,我们进行了实验来分析水彩颜料水滴在湿纸和冷冻纸上的沉降模式(图9)。从撞击时间到短暂阶段,直到最后的干燥状态,我们研究了油漆粘度、纸张粗糙度、纸张温度和释放水滴高度的变化。我们对可观察到的现象感兴趣,如油漆飞溅,扩散,指指,分支,流变沉积和分形图案,这些现象进行了详细研究,并根据控制参数进行了分类。在今年早些时候发表的一篇关于这一主题的论文中(Baron, Su和Vaidya, 2016),我们详细讨论了我们初步实验的结果。PI Vaidya和他的研究生David Baron一起致力于开发一个关于这个问题的理论模型。该模型基于从St. Venant方程(Yarin 2006;金、千,2001;Luu and Forterre, 2009)。得到的模型相当于一个初步的简单方程组:
dh ⁄ dt + 2哦 ⁄ R= 0;ρh杜 ⁄ dt= - tb;博士 ⁄ dt = U
式中,h、U、R分别为液滴扩散的高度、速度、半径与时间的关系;? 是流体的密度,b是基底剪应力,在这里也取决于温度。我们目前正在对这个系统进行数值求解,同时寻找合适的模型调整,以考虑由外部因素(如帆布的表面特征)引入的随机性。理论模型的目的是复制我们在实验中观察到的特征,并了解油漆材料特性对新出现的图案的影响。David碰巧也是一名画家,他打算利用这些调查来创作新的艺术作品,并在论文答辩时展出。
学生
- 阿曼达·利·菲利普斯,火狐体育研究生。
- Tevin Rouse -火狐体育研究生(2017硕士)
- Sajan Ramanathan -本科生/高中生
合作者

洛丽·麦肯
火狐体育音乐系

伊桑啊
纽约大学音乐体验设计实验室

亚当贝尔
卡尔加里大学音乐系

克劳斯·施尼策尔
火狐体育摄影系
出版物
期刊
- 张建军,苏海峰,张建军,涂料在干燥、潮湿和冷却表面上的飞溅动力学,流体力学学报,第1期,第2期,2016。
这些女士
- 特文·劳斯——运用随机过程的爵士乐即兴演奏(2017)
- 大卫·巴伦-水彩画的流体动力学:实验与建模(2017)
演讲
海报
- 排箫的数学:创造管道来匹配音符,(由Sajan Ramanathan提出),火狐体育第11届年度学生研究研讨会,海报展示,新泽西州火狐体育火狐体育,(2017)。大学生海报提名。
